pokerogue/docs/enemy-ai.md

# EnemyCommandPhase: How Enemy Pokémon Decide What to Do

## Step 1: Should the Enemy Pokémon Switch?

When battling an enemy Trainer, the first decision the enemy needs to make is whether or not to switch an active Pokémon with another Pokémon in their party. This decision is primarily made by comparing **matchup scores** between each Pokémon in the enemy's party.

### Calculating Matchup Scores

The core function for matchup score calculation can be found in `src/field/pokemon.ts`, within the `Pokemon` class:

```ts
getMatchupScore(pokemon: Pokemon): number;
```

This computes the source Pokémon's matchup score against the Pokémon passed by argument using the formula

$$\text{MUScore} = (\text{atkScore}+\text{defScore}) * \text{hpDiffRatio} $$

where
- $\text{atkScore}$ is the combined effectiveness of the source Pokémon's types against the opposing Pokémon's defensive typing: $\prod_{\text{types}} \text{typeEffectiveness}(\text{type}, \text{oppPokemon})$. $\text{typeEffectiveness}$ is 1 when the type deals neutral damage to the opposing Pokémon's defensive typing, 2 when the type deals super effective damage, and so on. $atkScore$ is also increased by 25 percent if the source Pokémon has a higher Speed stat than the opposing Pokémon.
- $\text{defScore}$ is the inverse of the opposing Pokémon's $\text{atkScore}$ against the source Pokémon's defensive typing, or $(\prod_{\text{types}} \text{typeEffectiveness}(\text{type}, \text{sourcePokemon}))^{-1}$. Unlike $\text{atkScore}$, $\text{defScore}$ is capped at a maximum score of 4.
- $\text{hpDiffRatio}= \text{sourceHpRatio}-\text{oppHpRatio}+1$. This is further multiplied by 1.5 if the source Pokémon has a higher Speed stat than the opposing Pokémon; however, $\text{hpDiffRatio}$ cannot be higher than 1.

The maximum possible matchup score a Pokémon could have against a single opponent is $(16+16)\times 2=64$, which occurs when
- the Pokémon hits its opponent for 4x super effective damage with both of its types.
- the Pokémon is immune to or resists both of the opponent's types by 4x.
- the Pokémon is at max HP while the opponent's HP ratio is near zero.

In most situations, though, a Pokémon's matchup score against an opponent will be at most 16, which is equivalent to having two super effective types and resisting both of the opponent's types with the same HP ratios as before.

The minimum possible matchup score a Pokémon could have against a single opponent is near zero, which occurs when the Pokémon's HP ratio is near zero while the opponent is at max HP. However, a Pokémon's matchup score can also be very low when its type(s) are 4x weak to and/or resisted by its opponent's types.

### Determining Switches in EnemyCommandPhase

The `EnemyCommandPhase` follows this process to determine whether or not an enemy Pokémon should switch on each turn during a Trainer battle.

1. If the Pokémon has a move already queued (e.g. they are recharging after using Hyper Beam), or they are trapped (e.g. by Bind or Arena Trap), skip to resolving a `FIGHT` command (see next section).
2. For each Pokémon in the enemy's party, [compute their matchup scores](#calculating-matchup-scores) against the active player Pokémon. If there are two active player Pokémon in the battle, add their matchup scores together.
3. Take the party member with the highest matchup score and apply a multiplier to the score that reduces the score based on how frequently the enemy trainer has switched Pokémon in the current battle.
   - The multiplier scales off of a counter that increments when the enemy trainer chooses to switch a Pokémon and decrements when they choose to use a move.
4. Compare the result of Step 3 with the active enemy Pokémon's matchup score. If the party member's matchup score is at least three times that of the active Pokémon, switch to that party member.
   - "Boss" trainers only require the party member's matchup score to be at least two times that of the active Pokémon, so they are more likely to switch than other trainers. The full list of boss trainers in the game is as follows:
     - All gym leaders, Elite 4 members, and Champions
     - All Evil Team leaders
     - The last three Rival Fights (on waves 95, 145, and 195)
5. If the enemy decided to switch, send a switch `turnCommand` and end this `EnemyCommandPhase`; otherwise, move on to resolving a `FIGHT` enemy command.

## Step 2: Selecting a Move

At this point, the enemy (a wild or trainer Pokémon) has decided against switching and instead will use a move from its moveset. However, it still needs to figure out which move to use and, if applicable, which target to use the move against. The logic for determining an enemy's next move and target is contained within two methods: `EnemyPokemon.getNextMove()` and `EnemyPokemon.getNextTargets()` in `src/field/pokemon.ts`.

### Choosing a Move with `getNextMove()`

In `getNextMove()`, the enemy Pokémon chooses a move to use in the following steps:
1. If the Pokémon has a move in its Move Queue (e.g. the second turn of a charging move), and the queued move is still usable, use that move against the given target.
2. Filter out any moves it can't use within its moveset. The remaining moves make up the enemy's **move pool** for the turn.
   1. A move can be unusable if it has no PP left or it has been disabled by another move or effect
   2. If the enemy's move pool is empty, use Struggle.
3. Calculate the **move score** of each move in the enemy's move pool.
   1. A move's move score is equivalent to the move's maximum **target score** among all of the move's possible targets on the field ([more on this later](#calculating-move-and-target-scores)).
   2. A move's move score is set to -20 if at least one of these conditions are met:
      - The move is unimplemented (or, more precisely, the move's name ends with " (N)").
      - Conditions for the move to succeed are not met (unless the move is Sucker Punch, Upper Hand, or Thunderclap, as those moves' conditions can't be resolved before the turn starts).
      - The move's target scores are 0 or `NaN` for each target. In this case, the game assumes the target score calculation for that move is unimplemented.
4. Sort the move pool in descending order of move scores.
5. From here, the enemy's move selection varies based on its `aiType`. If the enemy is a Boss Pokémon or has a Trainer, it uses the `SMART` AI type; otherwise, it uses the `SMART_RANDOM` AI type.
   1. Let $m_i$ be the *i*-th move in the sorted move pool $M$:
      - If `aiType === SMART_RANDOM`, the enemy has a 5/8 chance of selecting $m_0$ and a 3/8 chance of advancing to the next best move $m_1$, where it then repeats this roll. This process stops when a move is selected or the last move in the move pool is reached.
      - If `aiType === SMART`, a similar loop is used to decide between selecting the move $m_i$ and advancing to the next iteration with the move $m_{i+1}$. However, instead of using a flat probability, the following conditions need to be met to advance from selecting $m_i$ to $m_{i+1}$:
        - $\text{sign}(s_i) = \text{sign}(s_{i+1})$, where $s_i$ is the move score of $m_i$.
        - $\text{randInt}(0, 100) < \text{round}(\frac{s_{i+1}}{s_i}\times 50)$. In other words: if the scores of $m_i$ and $m_{i+1}$ have the same sign, the chance to advance to the next iteration with $m_{i+1}$ is proportional to how close the scores are to each other. The probability to advance to the next iteration is at most 50 percent (when $s_i$ and $s_{i+1}$ are equal).
6. The enemy will use the move selected in Step 5 against the target(s) with the highest [**target selection score (TSS)**](#choosing-targets-with-getnexttargets)

### Calculating Move and Target Scores

As part of the move selection process, the enemy Pokémon must compute a **target score (TS)** for each legal target for each move in its move pool. The base target score for all moves is a combination of the move's **user benefit score (UBS)** and **target benefit score (TBS)**.

![equation](https://latex.codecogs.com/png.image?%5Cinline%20%5Cdpi%7B100%7D%5Cbg%7Bwhite%7D%5Ctext%7BTS%7D=%5Ctext%7BUBS%7D&plus;%5Ctext%7BTBS%7D%5Ctimes%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D-1&%5Ctext%7Bif%20target%20is%20an%20opponent%7D%5C%5C1&%5Ctext%7Botherwise%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright.)

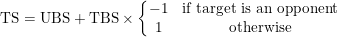
A move's UBS and TBS are computed with the respective functions in the `Move` class:

```ts
getUserBenefitScore(user: Pokemon, target: Pokemon, move: Move): integer;
getTargetBenefitScore(user: Pokemon, target: Pokemon, move: Move): integer;
```

Logically, these functions are very similar &ndash; they add up their respective benefit scores from each of the move's attributes (as determined by `attr.getUserBenefitScore`, and `attr.getTargetBenefitScore`, respectively) and return the total benefit score. However, there are two key functional differences in how the UBS and TBS of a move are handled:
1. In addition to influencing move selection, a move's TBS also influences target selection for that move, whereas UBS has no influence.
2. When evaluating the target score of a move against an opposing Pokémon, the move's TBS is multiplied by -1, whereas the move's UBS does not change. For this reason, move attributes return negative values for their TBS to reward using the move against an enemy.

#### Calculating Target Benefit Score (TBS) for Attack Moves

In addition to the base score from `Move.getTargetBenefitScore()`, attack moves calculate an `attackScore` which influences the move's TBS based on the following properties:
- The move's power (after the move's `VariablePowerAttrs` are applied)
- The move's type effectiveness against the target (note that this also accounts for type immunities from abilities such as Levitate and field effects such as Strong Winds).
- The move's category (Physical/Special), and whether the user has a higher Attack or Special Attack stat.

More specifically, the following steps are taken to compute the move's `attackScore`:
1. Compute a multiplier based on the move's type effectiveness: 

   ![typeMultEqn](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D%5Cbg%7Bwhite%7D%5Ctext%7BtypeMult%7D=%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D2&&%5Ctext%7Bif%20move%20is%20super%20effective(or%20better)%7D%5C%5C-2&&%5Ctext%7Botherwise%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright.)
2. Compute a multiplier based on the move's category and the user's offensive stats:
   1. Compute the user's offensive stat ratio:
      
      ![statRatioEqn](https://latex.codecogs.com/png.image?%5Cinline%20%5Cdpi%7B100%7D%5Cbg%7Bwhite%7D%5Ctext%7BstatRatio%7D=%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%5Cfrac%7B%5Ctext%7BuserSpAtk%7D%7D%7B%5Ctext%7BuserAtk%7D%7D&%5Ctext%7Bif%20move%20is%20physical%7D%5C%5C%5Cfrac%7B%5Ctext%7BuserAtk%7D%7D%7B%5Ctext%7BuserSpAtk%7D%7D&%5Ctext%7Botherwise%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright.)
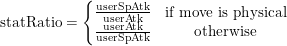
   2. Compute the stat-based multiplier:

      ![statMultEqn](https://latex.codecogs.com/png.image?%5Cinline%20%5Cdpi%7B100%7D%5Cbg%7Bwhite%7D%5Ctext%7BstatMult%7D=%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D2&%5Ctext%7Bif%20statRatio%7D%5Cle%200.75%5C%5C1.5&%5Ctext%7Bif%5C;%7D0.75%5Cle%5Ctext%7BstatRatio%7D%5Cle%200.875%5C%5C1&%5Ctext%7Botherwise%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright.)
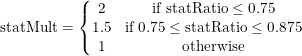
3. Calculate the move's `attackScore`:

   $\text{attackScore} = (\text{typeMult}\times \text{statMult})+\lfloor \frac{\text{power}}{5} \rfloor$

The maximum total multiplier in `attackScore` ($\text{typeMult}\times \text{statMult}$) is 4, which occurs for attacks that are super effective against the target and are categorically aligned with the user's offensive stats (e.g. the move is physical, and the user has much higher Attack than Sp. Atk). The minimum total multiplier of -4 occurs (somewhat confusingly) for attacks that are not super effective but are categorically aligned with the user's offensive stats.

The attack move's total TBS, then, is $\text{TBS}=\text{baseScore}-\text{attackScore}$, where $\text{baseScore}$ is the result of `Move.getTargetBenefitScore()`.

#### Calculating Target Score (TS) for Attack Moves

The final step to calculate an attack move's target score (TS) is to multiply the base target score by the move's type effectiveness and STAB (if it applies):
- If the target is an enemy, the corresponding TS is multiplied by the move's type effectiveness against the enemy (e.g. 2 if the move is super effective), then by 1.5 if the move shares a type with the user.
- If the target is an ally, the TS is divided by these factors instead.
- If $\text{TS}=0$ after these multipliers are applied, the TS is set to -20 for the current target.

### Choosing Targets with `getNextTargets()`

The enemy's target selection for single-target moves works in a very similar way to its move selection. Each potential target is given a **target selection score (TSS)** which is based on the move's [target benefit score](#calculating-move-and-target-scores) for that target:

![TSSEqn](https://latex.codecogs.com/png.image?%5Cinline%20%5Cdpi%7B100%7D%5Cbg%7Bwhite%7D%5Ctext%7BTSS%7D=%5Ctext%7BTBS%7D%5Ctimes%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D-1&%5Ctext%7Bif%20target%20is%20an%20opponent%7D%5C%5C1&%5Ctext%7Botherwise%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright.)

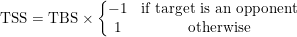
Once the TSS is calculated for each target, the target is selected as follows:
1. Sort the targets (indexes) in decreasing order of their target selection scores (or weights). Let $t_i$ be the index of the *i*-th target in the sorted list, and let $w_i$ be that target's corresponding TSS.
2. Normalize the weights. Let $w_n$ be the lowest-weighted target in the sorted list, then:
   
   ![normWeightEqn](https://latex.codecogs.com/png.image?%5Cinline%20%5Cdpi%7B100%7D%5Cbg%7Bwhite%7DW_i=%5Cleft%5C%7B%5Cbegin%7Bmatrix%7Dw_i&plus;%7Cw_n%7C&%5Ctext%7Bif%5C;%7Dw_n%5C;%5Ctext%7Bis%20negative%7D%5C%5Cw_i&%5Ctext%7Botherwise%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright.)
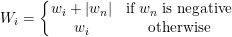
3. Remove all weights from the list such that $W_i < \frac{W_0}{2}$
4. Generate a random integer $R=\text{rand}(0, W_{\text{total}})$ where $W_{\text{total}}$ is the sum of all the remaining weights after Step 3.
5. For each target $(t_i, W_i)$,
   1. if $R \le \sum_{j=0}^{i} W_i$, or if $t_i$ is the last target in the list, **return** $t_i$
   2. otherwise, advance to the next target $t_{i+1}$ and repeat this check.

Once the target is selected, the enemy has successfully determined its next action for the turn, and its corresponding `EnemyCommandPhase` ends. From here, the `TurnStartPhase` processes the enemy's commands alongside the player's commands and begins to resolve the turn.

## An Example in Battle

Suppose you enter a single battle against an enemy trainer with the following Pokémon in their party:

1. An [Excadrill](https://bulbapedia.bulbagarden.net/wiki/Excadrill_(Pok%C3%A9mon)) with the Ability Sand Force and the following moveset
   1. Earthquake
   2. Iron Head
   3. Crush Claw
   4. Swords Dance
2. A [Heatmor](https://bulbapedia.bulbagarden.net/wiki/Heatmor_(Pok%C3%A9mon)) with the Ability Flash Fire and the following moveset
   1. Fire Lash
   2. Inferno
   3. Hone Claws
   4. Shadow Claw

The enemy trainer leads with their Heatmor, and you lead with a [Dachsbun](https://bulbapedia.bulbagarden.net/wiki/Dachsbun_(Pok%C3%A9mon)) with the Ability Well-Baked Body. We'll cover the enemy's behavior over the next two turns.

### Turn 1

To determine whether the enemy should switch Pokémon, it first calculates each party member's matchup scores against the player's Dachsbun:

$$\text{MUScore} = (\text{atkScore}+\text{defScore}) * \text{hpDiffRatio} $$
- Defensively, Heatmor's Fire typing resists Dachsbun's Fairy typing, so its `defScore` is 2. However, because of Dachsbun's Fire immunity granted by Well-Baked Body, Heatmor's `atkScore` against Dachsbun is 0. With both Pokémon at maximum HP, Heatmor's total matchup score is 2.
- Excadrill's Steel typing also resists Fairy, so its `defScore` is also 2. In this case, though, Steel is also super effective against Fairy, so Excadrill's base `atkScore` is 2. If Excadrill outspeeds Dachsbun (possibly due to it having a +Spd nature or holding a Carbos), its `atkScore` is further increased to 2.5. Since both Pokémon are at maximum HP, Excadrill's total matchup score is 4 (or 4.5 if it outspeeds).

Based on the enemy party's matchup scores, whether or not the trainer switches out Heatmor for Excadrill depends on the trainer's type. The difference in matchup scores is enough to cause a switch to Excadrill for boss trainers (e.g. gym leaders) but not for regular trainers. For this example, we'll assume the trainer is a boss and, therefore, decides to switch to Excadrill on this turn.

### Turn 2

Now that the enemy Pokémon with the best matchup score is on the field (assuming it survives Dachsbun's attack on the last turn), the enemy will now decide to have Excadrill use one of its moves. Assuming all of its moves are usable, we'll go through the target score calculations for each move:

- **Earthquake**: In a single battle, this move is just a 100-power Ground-type physical attack with no additional effects. With no additional benefit score from attributes, the move's base target score against the player's Dachsbun is just the `attackScore` from `AttackMove.getTargetBenefitScore()`. In this case, Earthquake's `attackScore` is given by
  
  $\text{attackScore}=(\text{typeMult}\times \text{statMult}) + \lfloor \frac{\text{power}}{5} \rfloor = -2\times 2 + 20 = 16$

  Here, `typeMult` is -2 because the move is not super effective, and `statMult` is 2 because Excadrill's Attack is significantly higher than its Sp. Atk. Accounting for STAB thanks to Excadrill's typing, the final target score for this move is **24**

- **Iron Head**: This move is an 80-power Steel-type physical attack with an additional chance to cause the target to flinch. With these properties, Iron Head has a user benefit score of 0 and a target benefit score given by
  
  $\text{TBS}=\text{getTargetBenefitScore(FlinchAttr)}-\text{attackScore}$

  Under its current implementation, the target benefit score of `FlinchAttr` is -5. Calculating the move's `attackScore`, we get:

  $\text{attackScore}=(\text{typeMult}\times \text{statMult}) + \lfloor \frac{\text{power}}{5} \rfloor = 2\times 2 + 16 = 20$

  Note that `typeMult` in this case is 2 because Iron Head is super effective (or better) against Dachsbun. With the move's UBS at 0, the base target score calculation against Dachsbun simplifies to

  $\text{TS}=-\text{TBS}=-(-5-20)=25$

  We then need to apply a 2x multiplier for the move's type effectiveness and a 1.5x multiplier since STAB applies. After applying these multipliers, the final score for this move is **75**.

- **Swords Dance**: As a non-attacking move, this move's benefit score is derived entirely from the sum of its attributes' benefit scores. Swords Dance's `StatChangeAttr` has a user benefit score of 0 and a target benefit score that, in this case, simplifies to

  $\text{TBS}=4\times \text{levels} + (-2\times \text{sign(levels)})$

  where `levels` is the number of stat stages added by the attribute (in this case, +2). The final score for this move is **6** (Note: because this move is self-targeted, we don't flip the sign of TBS when computing the target score).

- **Crush Claw**: This move is a 75-power Normal-type physical attack with a 50 percent chance to lower the target's Defense by one stage. The additional effect is implemented by the same `StatChangeAttr` as Swords Dance, so we can use the same formulas from before to compute the total TBS and base target score.
  
  $\text{TBS}=\text{getTargetBenefitScore(StatChangeAttr)}-\text{attackScore}$

  $\text{TBS}=(-4 + 2)-(-2\times 2 + \lfloor \frac{75}{5} \rfloor)=-2-11=-13$

  $\text{TS}=-\text{TBS}=13$

  This move is neutral against Dachsbun and isn't boosted by STAB from Excadrill, so we don't need to apply any extra multipliers. The final score for this move is **13**.

We now have a sorted move pool in decreasing order of move scores:
1. Iron Head (**75**)
2. Earthquake (**24**)
3. Crush Claw (**13**)
4. Swords Dance (**6**)

Since no other score is at least half that of Iron Head's score, the enemy AI automatically chooses to use Iron Head against Dachsbun at this point.

## Guidelines for Implementing Benefit Scores

When implementing a new move attribute, it's important to override `MoveAttr`'s `getUserBenefitScore` and `getTargetBenefitScore` functions to ensure that the enemy AI can accurately determine when and how to use moves with that attribute. Here are a few basic specifications you should adhere to when implementing benefit scores for a new attribute:
- A move's **user benefit score (UBS)** incentivizes (or discourages) the move's usage in general. A positive UBS gives the move more incentive to be used, while a negative UBS gives the move less incentive.
- A move's **target benefit score (TBS)** incentivizes (or discourages) the move's usage on a specific target. A positive TBS indicates the move is better used on the user or its allies, while a negative TBS indicates the move is better used on enemies.
- **The total benefit score (UBS + TBS) of a move should never be 0.** The move selection algorithm assumes the move's benefit score is unimplemented if the total score is 0 and penalizes the move's usage as a result. With status moves especially, it's important to have some form of implementation among the move's attributes to avoid this scenario.
- **Score functions that use formulas should include comments.** If your attribute requires complex logic or formulas to calculate benefit scores, please add comments to explain how the logic works and its intended effect on the enemy's decision making.